Navigating Medical Literature Part II: Critical Statistical Components to Understand

- written by Dr. Kevin Bunting Jr., PharmD (10-15 minute read)
All content in this post is for educational purposes only. Any content that aligns or matches any other sources is mere coincidence. All titles, examples and figures are made up and intentionally a little silly for demonstration purposes only.
If you missed Part I: Anatomy of a Journal Article, I recommend checking that out (HERE) before continuing on to this post.
You've made it to part 2! This is where literature review gets serious! Now it's time to begin learning how to analyze the nuance of the Results and Discussion sections with a scrutinizing eye.
Also, congrats on starting this post... this is a topic that is usually 1-2 semesters worth of material in graduate school... I will do my best to condense this down to what I feel are the most relevant and useful for our audience. If I miss any, or you'd like more details on a section feel free to email us at support@nesislabs.com or reach out to us on Instagram @nesislabs with any comments or questions! I personally respond to all inquiries!
Now, onto the post!
Just to recap my goals and to keep expectations for our roadmap on this three-part series:
I decided that I wanted to create a multi-part series to serve as a quick reference guide to analyzing some key items within peer-reviewed journal articles (i.e. what are the main sections of a journal article, what is a confidence interval? how do I know if a result shows statistical significant vs clinical significance, etc.).
Overview and what to expect:
-
Part I: Anatomy of a Journal Article (where you were last time)
-
Part II: Critical Statistical Components to Understand (where you are right now)
-
Part III: Drawing Your Own Conclusions (where you are going next)
Remember
It is not my goal to make everyone reading this a complete clinical expert. Trust me, it takes years of practice to develop a strong process for evaluating scientific scholarly journal articles.
It is my goal to make everyone reading this a bit more comfortable in reading and evaluating what you hear and see around you regarding the health and wellness space. I'd like you to be able to see a headline on social media or on the news and be able to ask appropriate questions to determine its validity and understand the nuance and magnitude of the claims you see.
Let's dig into more of the nuance of it by continuing with Part II: Critical Statistical Components to Understand
I will add commentary on my own personal approach to evaluating each of these sections as we move along this article.
1. Type of Study VS Level of Evidence
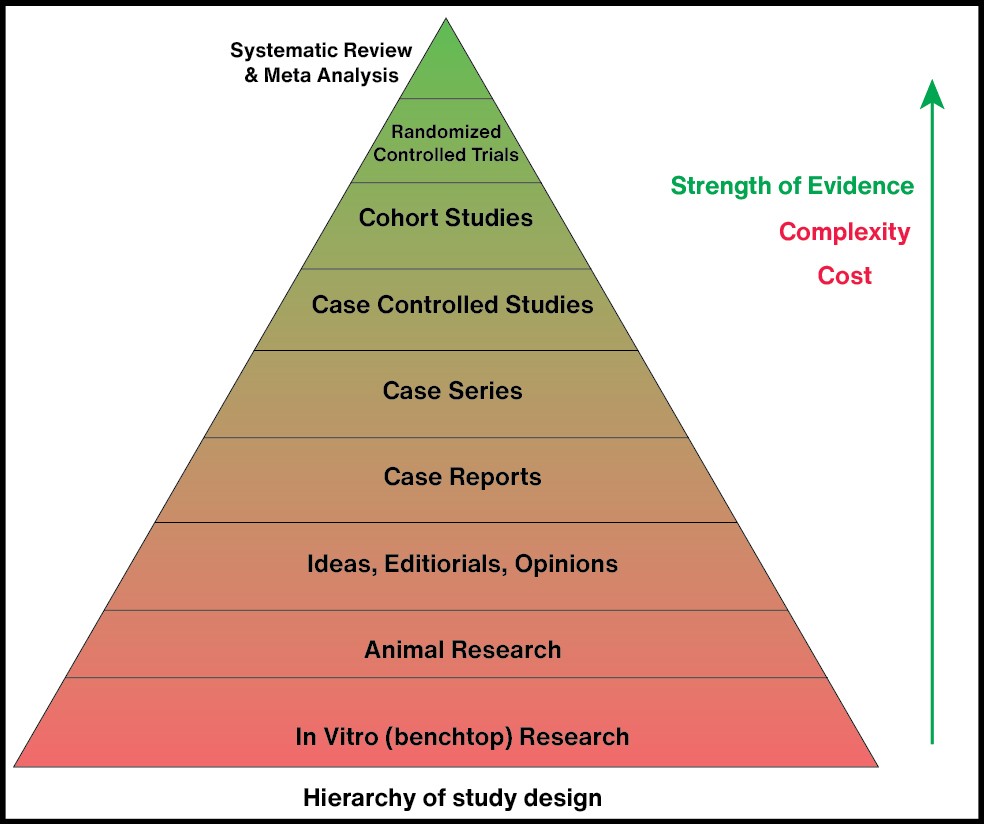
First and foremost, we need to understand what Type of study is being conducted. When you are within the Methods section of the article, it will typically list the Type under a subheading titled Study Design. When you see the name of the study design, the pyramid (pictured right on desktop, above if on mobile) should serve as a reference and pop into your head. What this pyramid shows is the balance between Strength of Evidence (top) at the cost of Complexity and Cost.
So, for example, a Randomized Controlled Trial (RTC) is considered stronger than Animal Research but at the cost of $$$ and complexity.
Below is a list of some of the more common study designs you may encounter and a brief definition of each:
-
In-Vitro Research: Investigates biological phenomena outside the living organism, typically involving the study of cells or tissues in a controlled laboratory environment.
-
Animal Research: Involves the use of animals to study biological systems, behaviors, or to test interventions, providing insights into potential applications into human health.
-
Ideas, Editorials, and Opinions: Presents authors' perspectives, opinions, or novel concepts in a non-systematic manner, often exploring hypotheses or discussing emerging trends without a formal research design.
-
Case Reports: Detailed descriptions of individual patient cases, highlighting unique or rare clinical presentations, interventions, and outcomes, often serving as valuable sources for hypothesis generation.
-
Case Series: A collection of multiple case reports, offering a broader overview of similar cases, providing cumulative evidence on a specific medical condition, treatment or intervention.
-
Case Controlled Studies: Compares individuals with a specific condition (cases) to those without it (controls) to explore potential associations between the condition and various factors, helping identify potential risk factors or protective elements.
-
Cohort Series: Follows a group of individuals (cohort) over time, tracking their exposure to certain variables, and observing outcomes to identify potential correlations or causal relationships.
-
Randomized Controlled Trial (RTC): Conducts a controlled experiment where participants are randomly assigned to different interventions or control groups, providing a robust method to assess the efficacy of treatments or interventions.
-
Systematic Review & Meta Analysis: A comprehensive review that systematically analyzes and synthesizes existing research on a specific topic, often incorporating statistical methods (meta-analysis) to provide a quantitative overview of the available evidence.
What I do: You're going to get sick of me saying this, but, I am not a 100% hard-and-fast rule setter for this area. It's more of a situational analysis that I complete when cross-referencing the strength of a study and its design. Since I am a co-founder of NESIS, my main area of expertise lately is within the dietary supplement and Contemporary and Alternative Medicine (CAM) space.
What this means is that MOST of the studies have a low number of participants (n) and are not powered to show statistical significance (see section 5 for description). That does NOT mean it's inherently bad. On average, a single participant will cost between $2,500 to $10,000 and to power a study, it may require hundreds if not thousands of participants. Most supplement companies cannot fund that type of study, and Big Pharma is not researching supplements. So, that means we need to use REASONABLE clinical judgement and assess the collective data available rather than simply demonizing slightly less strong evidence than an RCT.
Examples:
Gold Standard: RCT for a new FDA-approved medication.
Fine/Good: Case Controlled Study evaluating 200 graduate students ability to focus and retain information after taking 100 mg/kg of the amino acid L-tyrosine
May Raise Concern: ONLY In Vitro Research showing the botanical Dong Quai may increase breast cancer cell proliferation in petri dishes.
2. Definitions
Stick with me... this section is DENSE (sorry 😟)
Next, let's take a step back and build up our vocabulary. I want to make sure that when a term is being used, we have a reference point. I will be sure to expand on a few of these in the subsequent sections of this post. This list is not meant to be inclusive but is comprised of the common terms I see often.
-
Mean: The arithmetic average of a set of values, calculated by adding all values and dividing the sum by the total number of observations or data points.
-
Sensitivity: The proportion of TRUE POSITIVE results among individuals WITH a particular condition, reflecting a test's ability to correctly identify those with a condition.
-
Specificity: The proportion of TRUE NEGATIVE results among individuals WITHOUT a particular condition, indicating a test's ability to correctly identify those without the condition.
-
Standard Deviation: A measure of the dispersion or spread of a set of values, providing insight into how much individual values deviate from the mean. (described in section 3)
-
n: Number of participants, the sample size or number of observations within a study.
-
null-Hypothesis (Ho): A statistical hypothesis assuming NO EFFECT or NO DIFFERENCE, serving as the default assumption until evidence suggests otherwise. (described in section 4)
-
Hypothesis: A testable statement or proposition that suggests an expected relationship or outcome in a research study. (described in section 4)
-
Independent Variable: The variable manipulated or controlled by the researcher in an experiment or study; this is the PRESUMED CAUSE that is systematically varied to observe its effect ON THE DEPENDENT VARIABLE. (described in section 4)
-
Dependent Variable: The variable observed or measured IN RESPONSE TO CHANGED in the independent variable; this is the OUTCOME or RESPONSE that the researchers SEEK TO UNDERSTAND, explain or predict in the study. (described in section 4)
-
Cofounding Variable: An extraneous variable that may affect the observed relationship between the independent and dependent variables. (described in section 4)
-
Non-Modifiable Risk Factors: Characteristics or factors that contribute to an increased risk of a particular outcome but CANNOT be altered or controlled by intervention. (described in section 4)
-
Modifiable Risk Factors: Factors or behaviors that contribute to an increased risk of a particular outcome and CAN be altered or controlled through intervention. (described in section 4)
-
p Value: The probability that the observation is a result by chance. (described in section 5)
-
Confidence Interval (CI): A range of values that is likely to contain the TRUE value of an unknown parameter, providing a measure of the precision of an estimate. (described in section 5)
-
Power: The probability that a statistical test will CORRECTLY REJECT a FALSE NULL HYPOTHESIS (Ho) (a.k.a. the test's ability to detect a TRUE effect).
-
Type I Error: False Positive. Occurs when the null hypothesis (Ho) is INCORRECTLY REJECTED when it's ACTUALLY TRUE. This is denoted by the symbol alpha (α) and is usually set at 0.05 or a 5% chance.
-
Type II Error: False Negative. Occurs when the null-Hypothesis (Ho) is incorrectly NOT REJECTED when there is ACTUALLY a true effect. This is denoted by the symbol beta (ß).
-
Relative Risk: The ratio of the probability of an event occurring in one group compared to the probability in another group. (described in section 6)
-
Absolute Risk: The probability of an event occurring in a specific group or population providing a baseline measure WITHOUT considering a comparator group. (described in section 6)
-
Hazards Ratio: The ratio of the hazard rates between two groups in survival analysis, quantifying the risk of an event occurring at any time. (described in section 6)
-
Odds Ratio: The ratio of the odds of an event occurring in one group compared to the odds in another group, commonly seen in case controlled studies. (described in section 6)
-
Analysis of Variance (ANOVA): A statistical technique that assesses whether the MEANS of two or more groups are statistically DIFFERENT, typically used in studies designed with many groups. (described in section 7)
-
Chi-Squared Test: A statistical test that assess the association between CATEGORICAL variables, comparing the observed distribution of data with the expected distribution. (described in section 7)
-
Student's t-Test: A statistical test used to determine if the MEANS of TWO groups are SIGNIFICANTLY different from each other, commonly used with INDEPENDANT samples. (described in section 7)
-
Cox-Proportional Analysis: A statistical technique used for survival analysis, assessing the impact of MULTIPLE variables on the time until the event of interest occurs. (described in section 7)
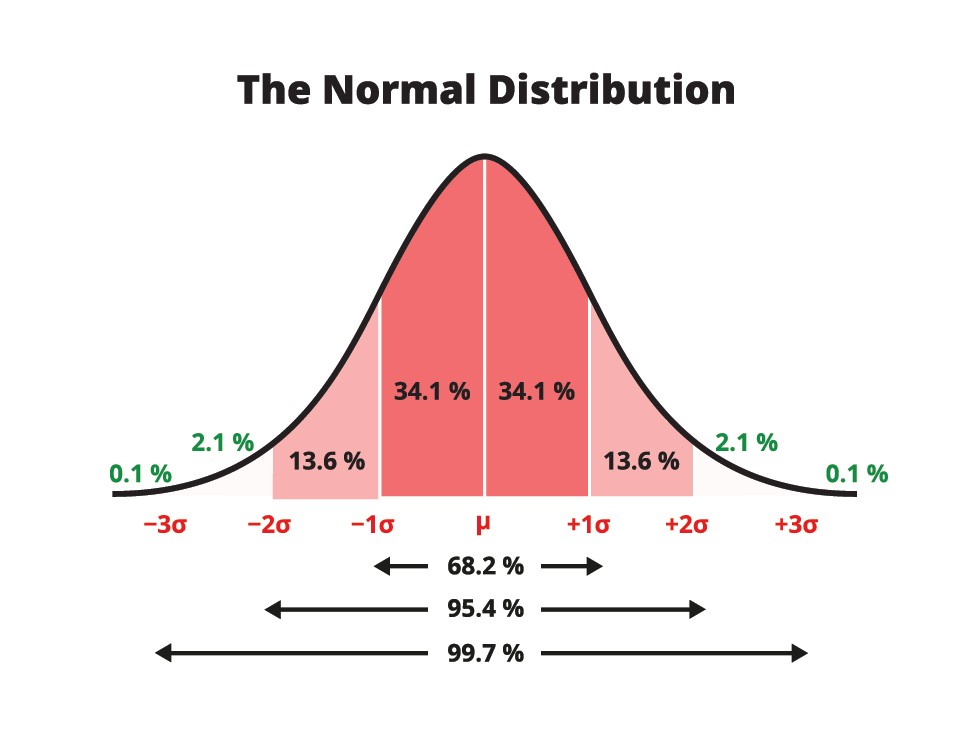
3. Standard Deviation & The Normal Distribution
The Standard Deviation (Σ) or (σ) is the statistical measure that observes the spread or dispersion of a set of variables around their Mean (µ). This is valuable to evaluate because it can show us the amount of variability within the study. The Normal Distribution Curve is often called the "Bell Curve Model" and is annotated showing each Standard Deviation with sigma (σ) value. This shows us what percentage of data falls within each section of the bell curve.
We can often ask ourselves when looking at complex data: "does this data follow a normally distributed model or is it skewed to one side or another?" Or, we can ask ourselves: "how many standard deviations from the mean are the results I am analyzing?"
A normally distributed model:
-
68% Rule (1σ): Approximately 68% of the data falls within one standard deviation of the mean. This signifies a moderate level of variability within the dataset.
-
95% Rule (2σ): Nearly 95% of the data falls within two standard deviations, representing a broader range and accounting for a more extensive spectrum of variability.
-
99.7% Rule (3σ): An overwhelming 99.7% of the data falls within three standard deviations, highlighting a vast majority of observations and encompassing a wide range of variability.
Now that we have the foundation, let's look at an example to see why this is important.
Imagine we're looking at the distribution of exam scores in a large class. The Mean score is 75, and the Standard Deviation is 10. Applying the sigma values:
-
68% Rule (1σ): Scores between 65 and 85 cover roughly 68% of the students, indicating that most students performed within this moderate range around the class average.
-
95% Rule (2σ): Expanding our range to 55–95 includes approximately 95% of the scores, encompassing a broader spectrum of student performance.
-
99.7% Rule (3σ): Now, considering scores from 45 to 105, an impressive 99.7% of the students fall within this extensive range, showcasing the full extent of variability in exam performance.
4. The Hypothesis, Variables & Risk Factors
When a researcher is designing a study, they typically begin with a question they are hoping to answer. Simply enough, this question is called the Hypothesis. Let's now assume that the Hypothesis is WRONG (i.e. we don't actually do the study), this assumption is called the null-Hypothesis (Ho).
Once the researcher has their question in mind, it's time to recruit and select their participants along with what exactly they will be measuring. There are variables that the researcher can manipulate (Independent Variable), the outcome they're measuring (Dependent Variable), and then (usually after the study (post hoc)) extraneous variables (Cofounding Variables).
OK, the researcher has their question, sample of participants and knows the outcome they will measure for, anything else to take into consideration?
Let's say there is a RISK associated with our intervention and we need to look deeper into our participants demographics to ensure we are not doing harm. The researcher may choose to look at Modifiable Risk Factors, or factors that CAN be changed with intervention (weight, lifestyle habits, diet, exercise routines, sleep schedule) versus the Non-Modifiable Risk Factors, or factors that CANNOT be changed with intervention (age, sex, race, pregnancy status* (grey area in the literature)).
Let's put this all together and design a study if we are this researcher:
We are interested in the impact of caffeine on reaction time.
Hypothesis: Participants who consume caffeine before a cognitive task will exhibit shorter reaction times compared to those who do not consume caffeine.
null-Hypothesis (Ho): There is no significant difference in reaction times between participants who consume caffeine and those who do not
Independent Variables: Amount of caffeine in each group
Dependent Variables: Measurement of reaction time in seconds (s) to press a buzzer when the participant sees an image appear on a screen
Cofounding Variables: Participants who take stimulant medications or work an overnight shift may show varied results compared to a participant who does not consume caffeine regularly and has a non-nocturnal sleep-wake cycle
Modifiable Risk Factors: We can identify sleep as a modifiable risk factor that can show negative results on poor nights of sleep
Non-Modifiable Risk Factor: Age can play a role in reaction time as our reaction time tends to decrease as we age
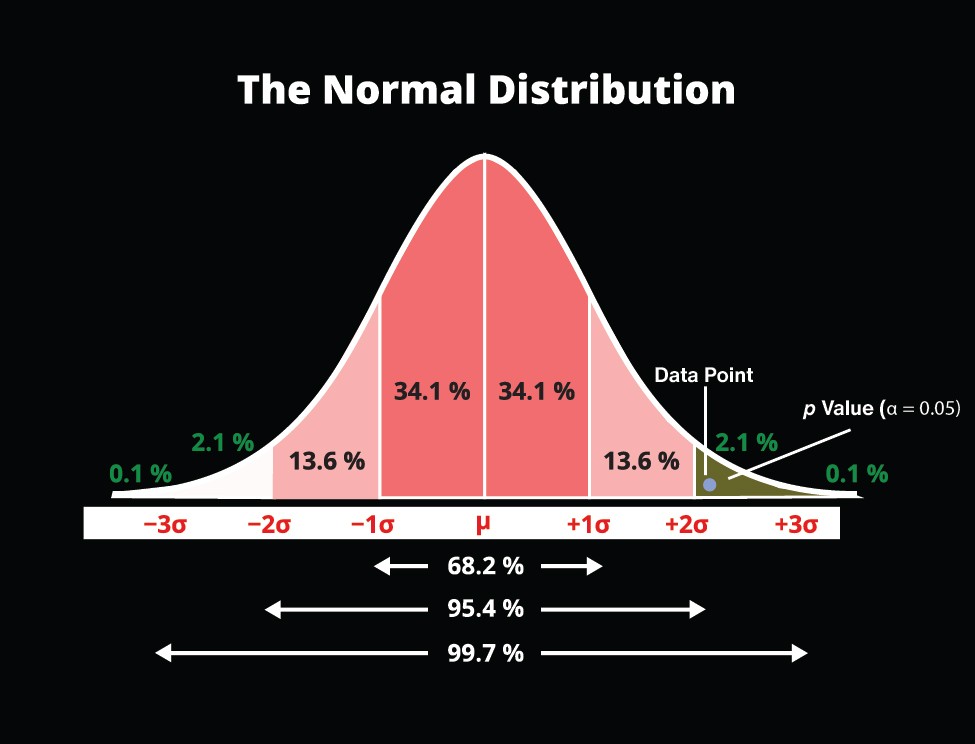
5. Determining Statistical Significance
OK, we've conducted our study and our biostatistician has given us the results (a.k.a. you're reading an article and are in the Results section of the paper). Upon first glace, it usually just looks like a bunch of numbers, Greek symbols, and brackets. Let's look at the important variables to determine if we have any sort of meaningful results here.
It's worth noting here that we needed to determine the appropriate Sample Size (n) to appropriately Power our study. There are complicated calculations called a Power Analysis that the research team does (should do) to ensure that their results can actually detect a meaningful difference between participants. This is a more behind the scenes aspect to articles, so I will not dive to deeply into it. We will assume our study has enough participants to detect a difference.
We will have an outcome we are looking at and the result will look something like this:
-
Outcome was changed by x (lower limit, upper limit) [95% CI, p<0.05]
Let's go back to our caffeine example to describe what these results mean: (Version 1 to show SIGNIFICANCE)
-
Consumption of 180 mg of caffeine improved reaction time by 0.5s (0.3, 1.2) [CI 95%, p = 0.01]
p Value: We set the threshold to < 0.05 and our result is 0.01, this means our results are NOT due to chance.
Confidence Interval: We are 95% confident that our results fall somewhere between 0.3s and 1.2s. This number is NOT less than or equal to 0 (no intervention), therefore, combining this p value and CI, these results ARE statistically significant.
Let's do another caffeine example to describe what these results mean: (Version 2 to show NO SIGNIFICANCE)
-
Consumption of 180 mg of caffeine improved reaction time by 0.5s (-0.3, 4) [CI 95%, p = 0.03]
p Value: We set the threshold to < 0.05 and our result is 0.03, this means our results are NOT due to chance.
Confidence Interval: We are 95% confident that our results fall somewhere between -0.3s and 4s. This number is less than or equal to 0 (no intervention), therefore, combining this p value and CI, these results are NOT statistically significant. In other words, JUST BECASUE our p value is less than our set value of 0.05, it does NOT automatically mean these results are significant.
Let's do one more caffeine example to describe what these results mean: (Version 3 to show CHANCE)
-
Consumption of 180 mg of caffeine improved reaction time by 0.5s (0.3, 1.2) [CI 95%, p = 0.4]
p Value: We set the threshold to < 0.05 and our result is 0.4, this means our results ARE due to chance and the data is NOT statistically significant.
6. Risks and Ratios
We will close this post out with a few more bullet-point overviews on some more advanced topics within biostatistics. These topics ARE important to recognize but not critical to know like the back of your hand. Some studies report one but not the others.
First, let's look at the different types of risks and ratios that can be reported (definitions from above are now below).
-
Relative Risk: The ratio of the probability of an event occurring in one group compared to the probability in another group.
-
Absolute Risk: The probability of an event occurring in a specific group or population providing a baseline measure WITHOUT considering a comparator group.
-
Hazards Ratio: The ratio of the hazard rates between two groups in survival analysis, quantifying the risk of an event occurring at any time.
-
Odds Ratio: The ratio of the odds of an event occurring in one group compared to the odds in another group, commonly seen in case controlled studies.
Now, let's apply all of these to our hypothetical caffeine study:
Let's say that we noticed a portion of our participants experiencing jitteriness post caffeine consumption which lead to decreased reaction times. Overall, we noticed a 15% chance that the caffeine group was going to experience delayed reaction times because of jitteriness vs 10% of the non-caffeine group attributed to nervousness. A hazards ratio of 1.8 was reported.
-
Relative Risk: In our caffeine study, we saw that that the risk of delayed reaction time in the group that consumed caffeine is 0.15, while in the non-caffeine group, it is 0.10. The Relative Risk would be 0.15 / 0.10 = 1.5. This implies that individuals in the caffeine group are 1.5 times more likely to experience delayed reaction times compared to those in the non-caffeine group.
-
Absolute Risk: If the Absolute Risk of delayed reaction time in the caffeine group is 0.15, it means that 15% of individuals in this group are expected to experience delayed reaction times.
-
Hazards Ratio: In our study we were monitoring reaction time over time, a hazards ratio of 1.8 was reported. It would suggest that individuals in the caffeine group have an 80% higher risk of delayed reaction times at any given point compared to the non-caffeine group.
-
Odds Ratio: If the odds of delayed reaction time in the caffeine group are 1:4 (1 event for every 4 non-events) and in the non-caffeine group are 1:8, the odds ratio would be (1/4) / (1/8) = 2. This indicates that the odds of experiencing delayed reaction times are twice as high in the caffeine group compared to the non-caffeine group.
7. BONUS: Overview of Some Statistical Tests
I wanted to throw in this bonus section to at least touch on some of the major statistical tests you may encounter when reading journal articles (definitions from above now below).
-
Analysis of Variance (ANOVA): A statistical technique that assesses whether the MEANS of two or more groups are statistically DIFFERENT, typically used in studies designed with many groups.
-
Chi-Squared Test: A statistical test that assess the association between CATEGORICAL variables, comparing the observed distribution of data with the expected distribution.
-
Student's t-Test: A statistical test used to determine if the MEANS of TWO groups are SIGNIFICANTLY different from each other, commonly used with INDEPENDANT samples.
-
Cox-Proportional Analysis: A statistical technique used for survival analysis, assessing the impact of MULTIPLE variables on the time until the event of interest occurs.
Now, let's apply all of these to our hypothetical caffeine study:
-
Analysis of Variance (ANOVA): We gave Group A 100 mg caffeine, Group B 150 mg caffeine, and Group C 200 mg caffeine. An ANOVA can be used to determine if there are statistically significant differences between these three groups.
-
Chi-Squared Test: If we categorize participants into fast, moderate, and slow reaction time groups, the Chi-squared test can reveal if caffeine consumption is distributed differently among these categories.
-
Student's t-Test: We can use this test to compare reaction times between participants who consumed caffeine and those who did not.
-
Cox-Proportional Analysis: If we want to explore the time until participants experience delayed reaction times, Cox-proportional analysis can help assess the impact of caffeine consumption.
And there you have it!
The Critical Statistical Components to Understand! Although this was quite lengthy, I only scratched the surface. This is a ton to digest and simply requires repetition and practice to master!
In fact, when I formulated NESIS INCEPTION, I went through this entire process for almost 200 peer-reviewed articles... It takes a lot of practice and persistence, but, if you stick with it, you'll get better!
Thank you for taking the time to read and learn with me!
Feel free to email us at support@nesislabs.com or reach out to us on Instagram @nesislabs with any comments or questions! I personally respond to all inquiries!



